衍生性商品風險管理 Derivatives Risk Management

財務工程在各個領域所著重的課題不盡相同，研究單位 (Quant Team) 希望能找到正確的評價模型，交易單位 (Trading Desk）希望能解讀市場的價格，風控單位 (Middle Desk) 則希望能掌握公司持有部位的風險。

這些通常隱含了許多調校 (Calibration)、插補 (Interpolation)、最佳化 (Optimization) 等複雜的數值運算，但回到源頭，其實每個單位想要知道的只是：「當市場發生變化時，衍生性商品部位的價值將會發生什麼變化。」

衍生性商品風險管理

Back to Basics

相信每一個學習過衍生性金融商品課程的學生都記得，在學習、了解各式各樣衍生性金融商品的評價模型之後，接下來一定是這些商品的風險係數 (Greeks) 推導，而不同的市場自然著重於不同的風險係數，像是股權市場 (Equity Market) 強調 Gamma、Vega 等風險，外匯市場 (FX Market) 則有 Vanna、Volga 等二階風險需要考量。

然而不管是什麼樣的風險係數，大家應該都還記得，這些都是依據泰勒展開式拆解出來的：

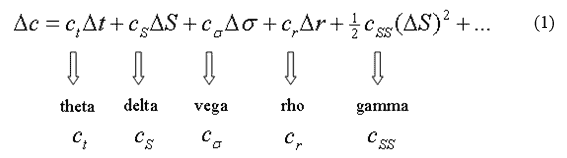
也就是說，我們先假設有哪些因素會影響選擇權的價值變化，而泰勒展開式的目的就是將這些因素個別或交互間，對選擇權價值變化的影響各自拆解開來，其中會有一階、二階乃至於高階的價值變化影響，但實務上我們只會考量在個別市場中具有顯著影響的風險係數。

廣義的來說，風險係數的定義如下：

風險係數	定義	風險階層
Delta	現貨價格變化對選擇權價值變化的影響程度	一階
Gamma	現貨價格變化對 Delta 變化的影響程度	二階
Vega	波動率變化對選擇權價值變化的影響程度	一階
Theta	存續時間變化對選擇權價值變化的影響程度	一階
Rho	無風險利率變化對選擇權價值變化的影響程度	一階
Vanna	現貨價格變化對 Vega 變化的影響程度	二階
Volga	波動率變化對 Vega 變化的影響程度	二階

認識風險

交易衍生性金融商品第一件要具備的就是，知道你的部位會受哪些因素影響，哪些風險是可以規避、可以藉由買賣現貨或是其他衍生性商品進行調整的，如 Delta、Gamma 風險等；有哪些風險是無法規避，雖然可以藉由買賣其他衍生性商品進行調整，但其成效卻難以評估的，如 Correlation 相關性風險；而有哪些風險難以衡量，理論上雖然有模型能夠評價，在實務上卻存有爭議的，如 Credit 信用風險。

知道你交易的商品種類會受哪些因素影響之後，接著就是將風險分類管理，交易員可以針對第一、二類的風險「Take View」買賣商品或調整其風險，風控單位需依照難以掌握的第二、三類風險對其獲利計提保留 (Provision)，而 Quant Team 則需要提供合理的方式拆解損益的來源。

分辨損益的來源 – P/L Break Down

為了讓交易員與風控單位明確的知道自己、公司的部位每天價值的波動來自於何種因素，究竟在 Delta 上賺多少錢、Gamma 輸了多少錢、而因為市場波動率的上升賠了多少錢，最簡單的方式就是用上述的 (1) 式拆解衍生性商品的價值。

由於實際市場隱含波動率存有微笑現象 (Smile Effect) 而非固定常數，若單純使用 (1) 式將會忽略「當現貨價格與波動率變化時，對隱含波動率曲線所造成的影響」，但對簡單的 PV (Plain Vanilla) 商品而言，若非快到期且在價平附近的部位^[1]，使用 (1) 式的估計能力都能落在誤差 5% ~ 10%^[2]以內。

然而對複雜的商品 (Exotics) 來說，尤以商品報酬型態具有跳躍風險 (Jump Risk) 者為甚，其 Vanna、Volga 風險更是可觀，外匯市場甚至為了考量這部分風險，在多年前提出了一種藉由 PV Option 調整其波動率風險，將調整量視為一種風險貼水加上原本的理論 Exotic 商品價格，可以視為一種超額避險 (Overhedge) 的評價法。

但即使取得風險貼水，將部位調整為 Vega 中立的情況下，整體部位的 Vega 風險依然會受到現貨價格與波動率變化的影響，也就是說，風險貼水是一回事，單純使用 (1) 式來解讀衍生商品部位的損益變化依然是不夠的。

對此，學界與業界提出了許多考量隨機波動率的模型，然而這類模型大多需要依照市場狀況，對模型參數進行調校 (Calibration)，也因此會造成模型解釋能力的不穩定性、最佳參數調校頻率等問題出現。

實務上，我們可以將原來的評價公式 BS(S, T, σ, fwd) 改為 BS(S, T, σ(S, T, ATM vol, R/R, fly), fwd)^[3]，並對此公式用泰勒展開式拆解出各個風險因素所造成的影響，即可得出較為合理且穩定的損益預估值。

將部分風險獨立控管

如上述所言，即便是簡單的 PV 商品，若是快到期且位於價平附近的部位，用再好的方式去拆解損益的變化依然無法獲得令人滿意的結果，因為這時交易員、公司所面臨的不再是模型能夠掌握的風險，而是所謂的履約風險 (Strike Risk)，這時候對交易員而言比較像是在「賭」現貨價格穿越履約價格的機率有多高，而在 FX 市場通常也會有所謂的 Fixing Risk，在 Fixing 的時間點^[4]時常會有外力出現影響市場價格。

對於複雜金融商品 (Exotics)^[5]來說，這類風險更為顯著，通常在現貨價格接近障礙價 (Barrier Price) 時，「賭」的成分也會相對提高，因此這類型的部位都需要獨立開來額外控管，不論對交易員或風控單位皆是如此。

風險管理案例 – 「從 GME 事件談裸賣選擇權」。

結語

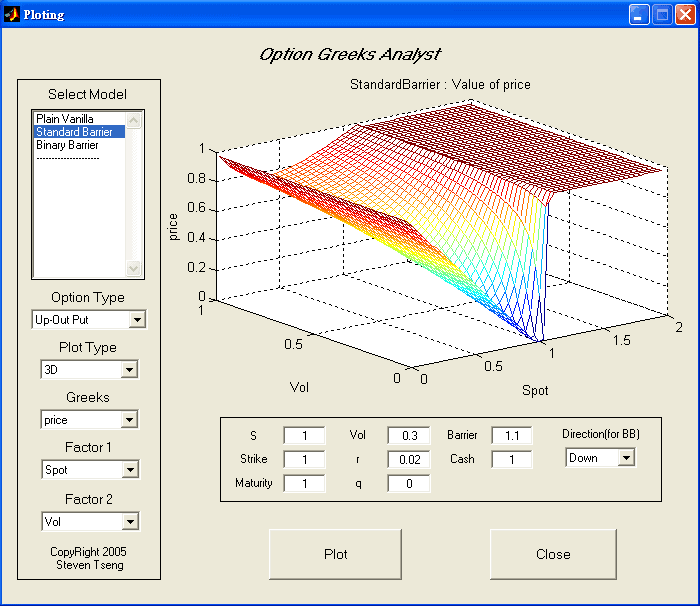
而唯有明確的知道各類型商品的風險分布情形為何，風控單位才能掌握公司部位損益的變動，從合理的角度與前台搭配，提出適合公司部位的風控管理辦法，這樣不僅能夠安全的管理，更能促進前台的業務發展。

---

[1] 這類的部位其風險需獨立控管，其說明請參照下文。

[2] 相對於每天損益的變化。 ex. 誤差 = (實際損益 – 估計損益) / 每日損益變動值

[3] 以 FX 市場為例。

[4] 以 FX Option 市場來說，Fixing 時間台幣為早上 11 點整，G7 為下午 2 點整。

[5] 如 Barrier、Double Barrier、Window Barrier、One Touch、Instant One Touch Option 等。