Python – 繪製選擇權的風險曲面 (Risk Profile)
在「衍生性商品風險管理 Derivatives Risk Management」一文中 (以下簡稱為前文),我們曾經討論過衍生性商品、選擇權的風險管理,透過泰勒展開式將影響選擇權的因子 – 選擇權標的物價格 (Price)、波動率 (Volatility)、存續時間 (Time) 等拆解出來。這些就是我們在交易選擇權時需要時刻注意,分析了解風險的分布以決定調整風險的時間與幅度。
本文將說明如何繪製風險曲面 (Risk Profile)。在開始之前,我們需要先把選擇權的評價函數、繪圖函數準備好。以下範例皆以 Python 編寫。
Python 程式碼
選擇權評價函數
在這我們參考「Python – 評價結構型商品 ELN & PGN」一文中已經介紹過的一般選擇權的評價函數,除了評價之外,我們把計算 Delta、Gamma 的部分加上。
from math import log, sqrt, exp
from scipy import stats
class bs_pv_option(object):
def init(self, S, K, r, T, sigma, b, CallPut, PorS):
...
def price(self):
...
def delta(self):
d1 = ((log(self.S / self.K) +
(self.b + 0.5 * self.sigma ** 2 ) * self.T) /
(self.sigma * sqrt(self.T)))
if self.CallPut == 1:
delta = exp((self.b - self.r) * self.T) * stats.norm.cdf(d1, 0.0, 1.0)
else:
delta = exp((self.b - self.r) * self.T) * (stats.norm.cdf(d1, 0.0, 1.0) - 1)
return delta * self.PorS
def gamma(self):
d1 = ((log(self.S / self.K) +
(self.b + 0.5 * self.sigma ** 2 ) * self.T) /
(self.sigma * sqrt(self.T)))
gamma = exp((self.b - self.r) * self.T) * (exp(-0.5 * d1 ** 2) /
(self.S * self.sigma * sqrt(self.T) * sqrt(2 * pi)))
return gamma * self.PorS其中類別中的 __init__ 函數決定了輸入參數的使用方式,並將參數傳遞給類別中的其他函數使用。
delta、gamma 函數則是使用 BS 模型,按照所輸入的股價、履約價、利率、選擇權天期、波動率等參數計算價格,並且將買賣方向 (PorS – purchase or sell) 也納入考量。
實務上,若選擇權、衍生性商品存在封閉解 (Closed Form),可以直接帶入偏微分公式計算即可 (如上)。若商品的結構較為複雜,存在路徑相依或事件相依的特性,則可以使用差分的方式計算處理。
Theoretical Greeks – 套用公式計算
Practical Greeks – 使用差分方式計算
其中對選擇權類型 CallPut 以及買賣方向 (PorS) 的處理要特別注意,如果在評價過程中想要將其作為參數,需要在變數型別的處理上特別用心。例如,若接收變數時為字串 ‘Call’ or ‘Put’ 但程式碼中計算需要轉換為 1 or -1。
風險曲面計算函數
以目前股價、選擇權存續時間為參考,計算股價、時間於向下與向上一個比率間的 delta、gamma 風險曲面。
from bs_option_class import *
import numpy as np
def opt_greeks_surface(Opt_func, S0, K, r, T, sigma, b, CallPut, PorS, greeks, H = None, RB = None, Type = None):
mat = np.linspace(0.05, T, 50)
Stock = np.linspace(S0 * 0.5 , S0 * 1.5, 50)
T, S = np.meshgrid(Stock, mat)
Opt_func == bs_pv_option or Opt_func == bs_digital_option:
o = Opt_func(S0, K, r, T, sigma, b, CallPut, PorS)
result = np.zeros_like(S)
for t in enumerate(mat):
for s in enumerate(Stock):
o.T = t[1]
o.S = s[1]
if greeks.upper() == 'D' or greeks.upper() == 'DELTA':
result[t[0], s[0]] = o.delta()
opt_type = 'Delta'
elif greeks.upper() == 'G' or greeks.upper() == 'GAMMA':
result[t[0], s[0]] = o.gamma()
opt_type = 'Gamma'
elif ...
return result, T, S, opt_type這邊利用到 python 的函數功能,可以將不同選擇權的函數名稱 (Opt_func) 與參數做為輸入參數,增加這個函數的使用彈性,不需要維護多個版本的 opt_greeks_surface 函數。
未來即使新增其他類型選擇權的評價類別,透過傳遞新類型選擇權的類別 (class) 名稱到 Opt_func 即可。
而後方參數的部分實際上也可以使用 **param 傳遞字典 (dict) 型態的變數,將選擇權評價公式中的參數存放在字典中即可。
風險曲面繪製函數
將取得的風險曲面數值 (result) 繪製為 3D 的曲面圖。
from pylab import cm, mpl, plt
from mpl_toolkits.mplot3d import Axes3D
def plot_greeks(T, S, result, greeks):
mpl.rcParams['font.family'] = 'serif'
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(T, S, result, rstride=1, cstride=1,
cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('Stock')
ax.set_ylabel('Maturity')
ax.set_title('Option '+greeks)這之中也可以加入額外參數決定繪製曲面圖的尺寸大小、是否要輸出儲存成圖檔等。
風險曲面繪圖
單一選擇權
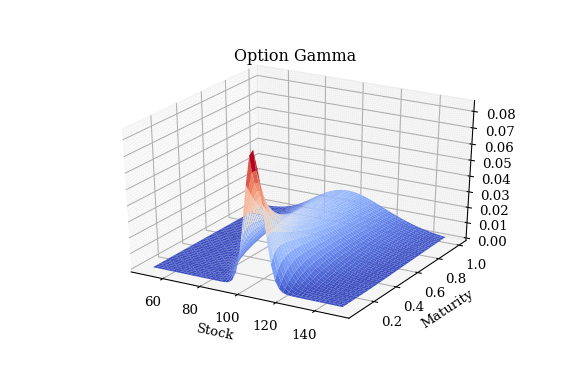
計算買入一般買權的 gamma 並繪圖:
result1, T, S, opt_type = opt_greeks_surface(bs_pv_option, 100, 105, 0.02, 1, 0.2, 0.02, 'Call', 'P', 'gamma')
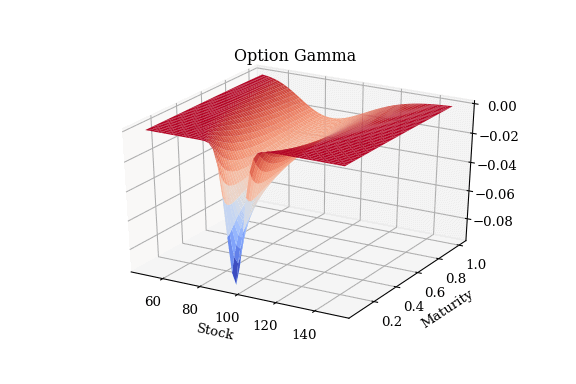
plot_greeks(T, S, result1, opt_type)計算賣出一般賣權的 gamma 並繪圖:
result1, T, S, opt_type = opt_greeks_surface(bs_pv_option, 100, 95, 0.02, 1, 0.2, 0.02, 'Put', 'S', 'gamma')
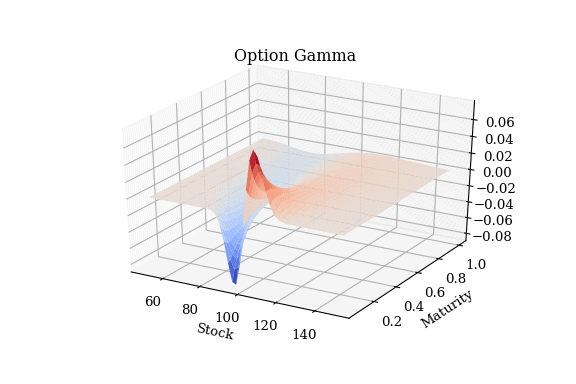
plot_greeks(T, S, result2, opt_type)買賣多筆選擇權 – 投資組合
將買入買權 + 賣出賣權的 gamma 曲面繪圖:
plot_greeks(T, S, result1+result2, opt_type)透過這樣的方式,我們就能順利的將各式各樣的衍生性商品、選擇權的風險曲面都繪製出來,方便前台交易員、中台風險管理人員能夠快速的理解手中握有部位的風險分布狀況,可以更好的掌握風險。
結語
作為「衍生性商品風險管理 Derivatives Risk Management」的延伸閱讀材料,透過本文的說明,希望大家能夠更進一步的了解如何繪製衍生性商品、選擇權的風險曲面。
當然,知道如何繪製並且能夠實際將風險曲面繪製出來只是第一步。接下來可以研究的還有:
- 更有效率的繪製風險曲面
- 如何更好的解讀風險分布
- 如何清楚的知道手中部位價值變化的損益歸因
這些我們再陸續跟大家說明。如果有任何問題,都歡迎留言討論喔!