Python – 評價結構型商品 ELN & PGN
在「結構型商品市場慣例 Structure Product Market Convention」一文中 (以下簡稱為前文),我們曾經討論過股權連結商品 (ELN) 與保本型商品 (PGN) 的交易與市場慣例,其概念就是透過固定收益商品 (定存或債券) 與選擇權的買賣組合讓投資人能夠參與選擇權標的股價的成長。
本文將詳細說明前文中 ELN 與 PGN 實務上要如何使用模型進行評價,計算其商品的百元價或按市價計價的價值 (MTM – Mark to Market)。以下範例皆以 Python 編寫。
Python 程式碼
由於前文範例的 ELN 與 PGN 中的選擇權為一般選擇權的賣權與買權,在這個範例中,我們需要將一般選擇權的評價模型準備好。
選擇權的理論評價模型:
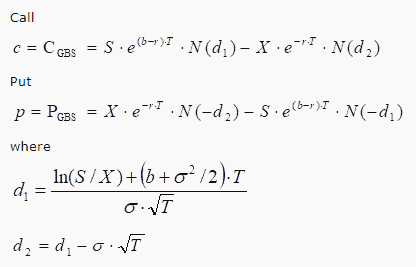
首先,使用類別 (class) 定義一般選擇權的評價函數。
from math import log, sqrt, exp
from scipy import stats
class bs_pv_option(object):
def init(self, S, K, r, T, sigma, b, CallPut, PorS):
...
def price(self):
d1 = ((log(self.S / self.K) +
(self.b + 0.5 * self.sigma ** 2 ) * self.T) /
(self.sigma * sqrt(self.T)))
d2 = d1 - (self.sigma * sqrt(self.T))
price = (self.CallPut * self.S * exp((self.b - self.r) * self.T) * stats.norm.cdf(self.CallPut * d1, 0.0, 1.0) -
self.CallPut * self.K * exp(-self.r * self.T) * stats.norm.cdf(self.CallPut * d2, 0.0, 1.0))
return price * self.PorS其中類別中的 __init__ 函數決定了輸入參數的使用方式,並將參數傳遞給類別中的其他函數使用。
price 函數則是使用 BS 模型,按照所輸入的股價、履約價、利率、選擇權天期、波動率等參數計算價格,並且將買賣方向 (PorS – purchase or sell) 也納入考量。
其中對選擇權類型 CallPut 以及買賣方向 (PorS) 的處理要特別注意,如果在評價過程中想要將其作為參數,需要在變數型別的處理上特別用心。例如,若接收變數時為字串 ‘Call’ or ‘Put’ 但程式碼中計算需要轉換為 1 or -1。
計算結構型商品價值
股權連結商品 ELN
按照前文中的範例,假設 ELN 合約名目本金為 10,000,000 元,其價值計算方式為:
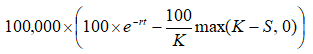
選擇權單位數為 100,000 × 100 / K = 10,000,000 / K,亦即為賣出10,000,000 / K 單位、轉換比率為 1:1 的賣權。
其中固定收益利率為 1%,選擇權期初股價為 50、履約價 53.5、市場利率為 2.5%、商品乘作天期為 35 天且定價波動率為 35%。
固定收益端百元價
假設到期時拿回 100,以固定收益利率折現到評價日當天的現值計算方法為:
100 * exp(-0.01 * 35/365) = 99.90415554920403因此,可以預期固定收益端的利息為 0.09584445079596549。(實務上,操作時會按實際交易的利率商品的計息方式計算)
四捨五入後即為前文中的百元價 99.90、利息 0.1。
選擇權端百元價
選擇權端則需考量百元價的單位數為 100 / K,再乘上選擇權價值後即為:
option = bs_pv_option(50, 53.5, 0.025, 35/365, 0.35, 0.025, 'Put', 'S')
100/53.5 * option.price() = -8.06025493674632四捨五入後即為前文中的百元價 8.06。
合約百元價
將固定收益端與選擇權端整體考量後,才是 ELN 的合約百元價:
100 * exp(-0.01 * 35/365) + 100/53.5 * option.price()
= 99.90415554920403 - 8.06025493674632
= 91.84390061245772四捨五入後即為前文中的百元價 91.84。
即是投資人於期初需先支付的商品價金 91.84 x 100,000 = 9,184,000 元。
也就是說,ELN 的投資者買的是一個希望標的股價在 35 天後不會低於履約價的機會,當股價不低於履約價時則可以獲得賣出選擇權的收益。
相對的,當股價低於履約價的時候,可以視同為將名目本金用履約價轉換為約當的標的股票。實務上可能是用現金或實際股票結算,端看期初簽訂的買賣合約而定。
大家也可以思考一下,這商品結構是不是跟雙元貨幣存款 (DCI – Dual Currency Investment) 看起來有 87 分像呢? 沒錯,DCI 實際上也是讓投資人、存戶賣出選擇權以獲取增強的利息收益的。(其實就是權利金)
因為貨幣、外匯選擇權的屬性比較特別一些,我們留待未來的文章或課程中再來跟大家詳細說明。
保本型商品 PGN
按照前文中的範例,假設 PGN 合約名目本金為 10,000,000 元,90% 保本,其價值計算方式為:
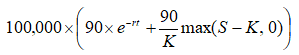
選擇權單位數為 100,000 × 90 / K = 9,000,000 / K,亦即為買入 9,000,000 / K 單位、轉換比率為 1:1 的買權。
其中固定收益利率為 1%,選擇權期初股價為 50、履約價 50、市場利率為 2.5%、商品乘作天期為 365 天且定價波動率為 27.57%。
固定收益端百元價
假設到期時拿回 90 (保本價),以固定收益利率折現到評價日當天的現值計算方法為:
90 * exp(-0.01 * 365/365) = 89.10448503742514所以可以預期固定收益端的利息為 0.8955149625748646。(實務上,操作時會按實際交易的利率商品的計息方式計算)
四捨五入後即為前文中的百元價 89.104、利息 0.896。
選擇權端百元價
選擇權端則需考量百元價的單位數為 90 / K,再乘上選擇權價值後即為:
option = bs_pv_option(50, 50, 0.025, 365/365, 0.2757, 0.025, 'Call', 'P')
90/50 * option.price() = 10.896714769592341四捨五入後即為前文中的百元價 10.897。
合約百元價
將固定收益端與選擇權端整體考量後,
90 * exp(-0.01 * 365/365) + 80/50 * option.price()
= 89.10448503742514 + 10.896714769592341
= 100.00119980701747四捨五入後即為前文中的百元價 100.00。
即是投資人於期初需先支付的商品價金 100.00 x 100,000 = 10,000,000 元。
換句話說,PGN 的投資者買的是一個希望標的股價在 365 天後能高於履約價的機會,因為保本比率為 90% 代表著使用較多的成本投資在選擇權的部分,因此到期時股價需要高於履約價一定比率才能拿回期初投資本金,達到損益兩平。
當然,也因為是保本型商品,到期時不管股價低於履約價多少 %,都能夠有 90% 的本金保障,可以視同為具有下檔保護的投資。這類商品一般都是採用現金的方式結算。
結語
作為「結構型商品市場慣例 Structure Product Market Convention」的延伸閱讀材料,透過本文的說明,希望大家能更進一步的了解結構型商品 ELN 與 PGN 的評價方式以及財務工程實作上我們需要準備的基礎材料有哪些。
同樣的,如果券商、銀行所發行的結構型商品中所包含的選擇權是其他類型的選擇權,例如數位選擇權或障礙選擇權等,基本上只需要將上述 Python 程式碼中描述的選擇權評價函數改為數位或障礙選擇權即可。
後續我們再從風險分析的角度,計算當市場狀況 (包含股價、利率、時間、波動率等) 改變時,商品價值變化的損益歸因。
歡迎訂閱 Quants Note 電子報、按讚 Facebook 粉專,持續獲得最新的資訊。






考慮寫寫看TRF嗎?
有規劃一系列的文章想要寫寫更複雜一些的結構型商品,包含 TRF、RA 以及一些只能透過 Monte Carlo simulation 才能評價的商品,但這一年來工作繁忙所以擱置了 XD