Python – 繪製選擇權的收益曲線 (Payoff Diagram)

在「Derivatives Building Block 新金融商品設計的 3 種方式」一文中，我們談論過如何透過融合的方式，利用簡單型態的選擇權，組裝出新商品。

在研究、設計金融商品時，可以透過了解既有商品的特性，選擇投資人偏好的元素將之組合形成新商品；這些商品的特性包含：

• 成本 / 收益
  成本與收益為一體之兩面，投資人通常會偏好帶有高收益報酬的商品；而發行商為了迎合投資人的喜好，則會需要增加其他特性來減少選擇權的成本。
• 時間
  跟時間有關的特性，例如，障礙價 (Barrier Level)。在選擇權存續期間，標的股價碰觸到障礙價之後選擇權才會生效、失效，這類特性可以讓選擇權成本 (價格) 降低。

從商品的收益面著手會是最為方便，也最容易能讓人理解金融商品的組成元素。工欲善其事，必先利其器。在開始之前，我們先要把基本選擇權的收益曲線函數、繪圖函數準備好，以下範例皆由 Python 編寫。

Python 程式碼

收益曲線 (Payoff Diagram)

使用類別 (class) 定義各類型選擇權的收益曲線函數以及相關評價函數。

一般選擇權 (Plain Vanilla Option) – 買/賣權

一般選擇權的收益計算方式為：

• 買權
  Max( 股價 (S) – 履約價 (K), 0)
• 賣權
  Max( 履約價 (K) – 股價 (S), 0)

class bs_pv_option(object):
    def __init__(self, S, K, r, T, sigma, b, CallPut, PorS):
        ...

    def payoff(self):
        payoff = max(self.CallPut * self.S - self.CallPut * self.K, 0)
        return payoff * self.PorS

其中類別中的 __init__ 函數決定了輸入參數的使用方式，並將參數傳遞給類別中的其他函數使用。

payoff 函數相對簡單，只需要考慮按上述收益計算邏輯判斷買賣權的收益報酬，並且將買賣方向 (PorS – purchase or sell) 也納入考量。

數位選擇權 (Digital Option) – 買/賣權

數位選擇權的收益計算方式為：

• 買權

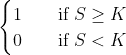
• 賣權

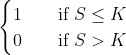
class bs_digital_option(object):
    def __init__(self, S, K, r, T, sigma, b, CallPut, PorS):
        ...

    def payoff(self):
        payoff = 1 if (self.CallPut * self.S - self.CallPut * self.K) >= 0 else 0
        return payoff * self.PorS

對於數位選擇權而言，收益計算是二元性的。因此 payoff 函數也是根據股價與履約價的關係，判斷是否在價內 (ITM – in the money) 即可，同時也將買賣方向納入考量。

繪圖函數

計算區間內股價的選擇權收益曲線

以目前股價為參考，計算股價於向下 80% 到向上 120% 間的選擇權收益曲線。

from bs_option_class import *
import numpy as np

def opt_payoff(Opt_func, S0, K, r, T, sigma, b, CallPut, PorS, H = None, RB = None, Type = None):
    Stock = np.linspace(S0 * 0.8, S0 * 1.2, 500)

    o = Opt_func(S0, K, r, T, sigma, b, CallPut, PorS)
    result = np.zeros_like(Stock)

    for s in enumerate(Stock):
        o.S = s[1]
        result[s[0]] = o.payoff()
    return result, Stock

這邊利用到 python 的函數功能，可以將不同選擇權的函數名稱 (Opt_func) 與參數做為輸入參數，增加這個函數的使用彈性，不需要維護多個版本的 opt_payoff 函數。

未來即使新增其他類型選擇權的評價類別，透過傳遞新類型選擇權的類別 (class) 名稱到 Opt_func 即可。

而後方參數的部分實際上也可以使用 **param 傳遞字典 (dict) 型態的變數，將選擇權評價公式中的參數存放在字典中即可。

繪圖

將取得的收益 (result) 繪製為 2D 的曲線圖。

from pylab import plt

def plot_payoff(Stock, result):
    plt.figure(figsize=(10, 6))
    plt.plot(Stock, result)
    plt.xlabel('Price')
    plt.ylabel('Payoff')
    plt.title('Option Payoff')

將股價區間與收益曲線的結果做為輸入參數，並進行繪圖。

收益曲線繪圖

一般買、賣權與組合策略

計算買入一般買權的收益並繪圖：

result1, Stock = opt_payoff(bs_pv_option, 100, 105, 0.02, 1, 0.2, 0.02, 'Call', 'P')
plot_payoff(Stock, result1)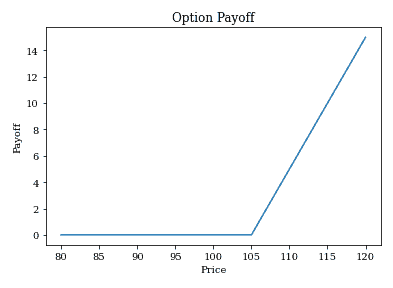

計算買入一般賣權的收益並繪圖：

result2, Stock = opt_payoff(bs_pv_option, 100, 95, 0.02, 1, 0.2, 0.02, 'Put', 'P')
plot_payoff(Stock, result2)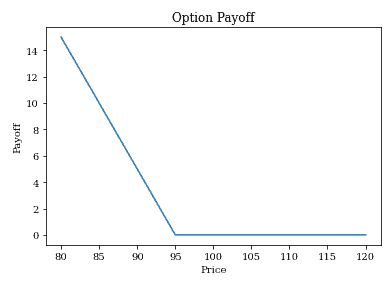

將買入買權 + 買入賣權的收益繪圖：

plot_payoff(Stock, result1+result2)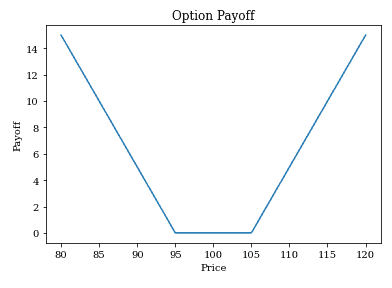

這也稱為選擇權的勒式組合 (Strangle)，一般會用於對未來市場行情有大漲或大跌的看法時使用，支付權利金以換取大漲、大跌後的報酬。相對的，如果選擇權到期時股價沒有超過買、賣權的履約價區間 (95 – 105)，則會損失權利金。

數位選擇權與組合策略

計算買入數位選擇權買權的收益並繪圖：

result3, Stock = opt_payoff(bs_digital_option, 100, 95, 0.02, 1, 0.2, 0.02, 'Call', 'P')
plot_payoff(Stock, result3)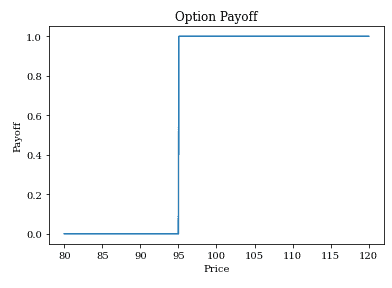

計算買入數位選擇權賣權的收益並繪圖：

result2, Stock = opt_payoff(bs_digital_option, 100, 105, 0.02, 1, 0.2, 0.02, 'Put', 'P')
plot_payoff(Stock, result2)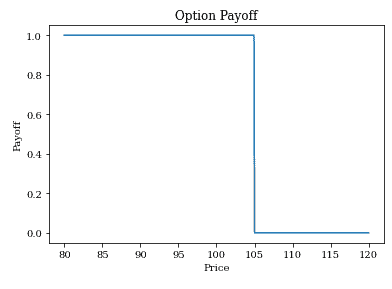

將多個買入數位選擇權買權 + 賣權的收益繪圖：

result1, Stock = opt_payoff(bs_digital_option, 100, 85, 0.02, 1, 0.2, 0.02, 'Call', 'P')
result2, Stock = opt_payoff(bs_digital_option, 100, 105, 0.02, 1, 0.2, 0.02, 'Put', 'P')
result3, Stock = opt_payoff(bs_digital_option, 100, 95, 0.02, 1, 0.2, 0.02, 'Call', 'P')
result4, Stock = opt_payoff(bs_digital_option, 100, 115, 0.02, 1, 0.2, 0.02, 'Put', 'P')
plot_payoff(Stock, result1+result2+result3+result4)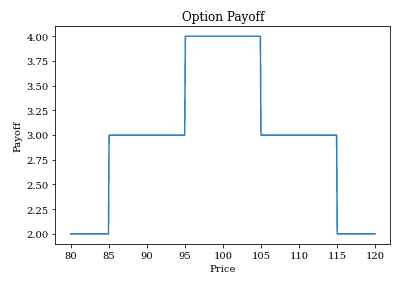

這就是我們在 Derivatives Building Block (關於金融商品設計) 一文中所提到的結婚蛋糕 (Wedding Cake) 商品了，透過饒富趣味的收益計算方式吸引投資人的注意。

當選擇權到期時，股價介於小區間內 (95 – 105) 可獲得最高的收益，介於 85 – 115 之間則可以獲得次高的收益。一般會用於對未來市場行情走勢的看法為區間內盤整時使用。

結語

作為 Derivatives Building Block (關於金融商品設計) 的延伸閱讀材料，透過本文的說明，希望大家能更進一步的了解金融商品設計的過程以及財務工程實作上我們需要準備的基礎材料有哪些。

財務工程是需要複合能力的有趣工作，除了金融業的知識之外，還需要數學建模以及編寫程式碼實作。而觸及的領域更是多不勝數，其他方面的話題就有待我們日後持續與大家分享了。