Derivatives Building Block 新金融商品設計的 3 種方式
在「同質性避險策略 Hedging with Homogeneity」一文中,曾經介紹過一種設計、創造新商品的流程概念,藉由了解已知商品的詳細風險分布,配合發行商的風險偏好,即可創造出有利於發行商與投資人的「新」型態商品。事實上,金融市場日新月異,隨時都有許多新型態的商品 (Exotic Options) 問世,而創造新商品的方式不外乎有:
- 創新 – 從無中生有
- 變形 – 改造既有商品
- 融合 – 使用既有商品組裝成新商品
而本文的主題將著重於第三種方式,利用既有商品為基石、以疊床架屋的方式,組裝出新型態的商品。
金融商品的基本元素 (Building Block)
為了使用「融合」的方式創造商品,我們必須先對商品的基本元素有廣泛的認識,通常這些組成元素大多是一般型態選擇權 (Plain Vanilla Option) 或是簡單型態的 Exotic Option,藉由了解這些組成元素的商品條件與特性,我們才有辦法從中選取、組合成想要的商品形態。接下來我們先介紹幾種簡單型態的選擇權:
A. Plain Vanilla Option
即為一般的歐式選擇權,藉由買進與賣出不同買權、賣權的組合,可創造出許多策略交易組合,如跨式、勒式等部位。因非本文重點,在此並不多加贅述。
B. Digital Option
數位選擇權,於到期日當股價超過某一水準 (履約價) 時,選擇權的買方即可收取一固定現金金額,而選擇權賣方則須在到期日支付此固定現金金額。常見的有 Wedding Cake (結婚蛋糕)、Range Accrual (區間計息) 等衍生商品。
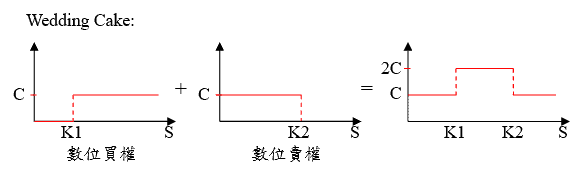
藉由買進不同履約價的數位買權、賣權,即可一層一層的疊出結婚蛋糕的形狀。
C. Barrier Option
障礙選擇權,可分為向上、向下,出局或入局的障礙買權與賣權,共有八種型態,為了簡化說明,在此僅介紹與後續內容相關的向上出局買權 (Up-Out Call) 與向上出局賣權 (Up-Out Put)。顧名思義,此類型買、賣權即為一般買、賣權加上一障礙條件,於選擇權存續期間內,一旦股價碰觸到障礙價位,則選擇權立即失效,而買方則可獲得一固定金額的Rebate (此金額亦可以為 0);若未曾碰觸障礙價位,則以一般買、賣權的方式履約。
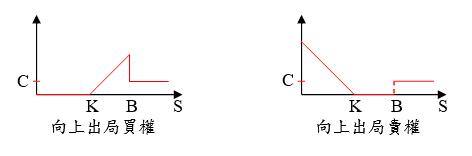
D. Binary Barrier Option
二元障礙選擇權,依照 Reiner、Rubenstein (1991) 的論文,此類型選擇權共有 28 種型態,因為包含許多支付型態為數位式的障礙選擇權,因此被命名為「二元」障礙選擇權。為了簡化說明,在此僅介紹與後續內容相關的 No Touch Option。同樣的,這種選擇權則是在存續期間內,股價一旦碰觸到障礙價格,則選擇權立即失效;若未曾碰觸障礙價格,選擇權買方則可於到期時獲得一固定現金金額。
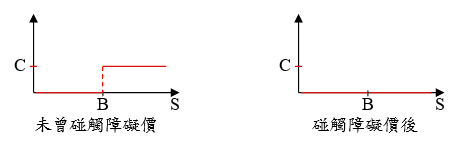
障礙選擇權與二元障礙選擇權在應用上的價值相當的高,是相當實用的組成元素,在搭配其他選擇權下,其衍生商品有可拆解的 Type 1 Knock-In-Knock-Out Option (KIKO) 以及前些年券商曾發行的累積鎖利結構型商品等,詳細內容請見下文。
E. Double-Knock-Out Option、Double-No-Touch Digital Option
雙重出局選擇權,與一般障礙選擇權相仿,不同的是其障礙價位有兩個,於選擇權存續期間內,一旦股價碰觸到任一個障礙價位,則選擇權立即失效,而買方則可獲得一固定現金金額 (此金額亦可以為0);若未曾碰觸障礙價位,則以一般買、賣權的方式履約。
Double-No-Touch Digital 選擇權則與雙重障礙選擇權類似,不同的是當股價於存續期間內碰觸到任一個障礙價位,則選擇權立即失效;若未曾碰觸障礙價位,選擇權買方則可獲得一固定現金金額。
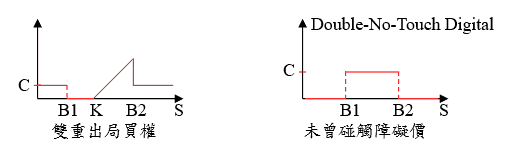
常見的衍生商品有 Onion Option (洋蔥選擇權) 等。
創造新商品
有了上述幾種基本元素之後,我們可以開始組裝出其他型態的商品。接下來將介紹 KIKO、累積鎖利結構型商品、洋蔥選擇權與上述組成元素之間的關係。
KIKO (Knock-In-Knock-Out Option, Type 1)
KIKO 是同時擁有出局與入局條件的障礙選擇權,選擇權存續期間內當股價一旦碰觸到出局障礙價位時,則選擇權立即失效,然而若選擇權未曾碰觸入局障礙價位,則到期選擇權亦將不具任何價值。因此在未曾碰觸出局條件,且至少碰觸一次入局條件的情形下,到期時才會以一般買、賣權的方式履約。假設 L 為出局障礙價位,U 為入局障礙價位。
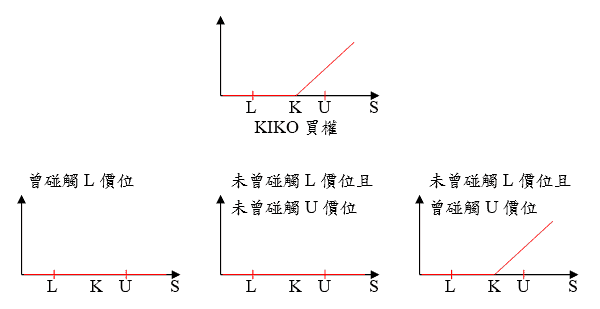
這類型選擇權可拆解為同時買進向下出局買權 (Down-Out-Call) 且賣出雙重出局買權 (Double-Knock-Out Call):
KIKO(L, U) = DOC(L) – DKOC(L, U)
一旦股價曾經碰觸出局價位 L,則向下出局買權與雙重出局買權同時失效,若未曾碰觸 L 與 U 價位,則到期兩個選擇權都成為一般買權,相互抵銷。當未曾碰觸 L 價位,且曾碰觸 U 價位時,雙重出局買權失效,而向下出局買權將於到期日轉變為一般買權。
累積鎖利結構型商品

此商品為 124 個選擇權 (121天期) 所組成,買進此商品可視同為:
- 賣出一個 121 天期的 No Touch Option
- 買進一系列 1~121 天期,共 121 個 No Touch Option
- 買進一個 121 天期的 Up-Out-Call
- 賣出一個 121 天期的 Up-Out-Put
其履約價格為 94%,觸及價格為 108%,長天期 No Touch Option 的 Rebate 為 (108% – 94%) / 94% = 14.8936%,一系列短天期 No Touch Option 的 Rebate 則為 14.8936% / 121。
因此,在選擇權存續期間內,當股價維持在觸及價格之下時,一系列短天期 No Touch Option 將會逐一失效 (一天一個),投資人每天將可累積 14.8936% / 121 的收益率,若於存續期間內穿越觸及價格,則向上出局買、賣權,長天期 No Touch Option 與剩下的一系列短天期 No Touch Option 將同時失效,至此契約結束,投資人將可拿到總計14.8936% / 121 * n 的提前到期報酬。
若股價未曾穿越觸及價格,到期日時所賣出的長天期 No Touch Option 須支付 14.8936%,將與先前一系列短天期 No Touch Option 所累積的金額相互抵銷。另一方面,若到期日股價高於履約價,則向上出局賣權不具價值,投資人將以一般買權履約;若到期日股價低於履約價,則向上出局買權不具價值,投資人將以一般賣權履約。
洋蔥選擇權 (Onion Option)
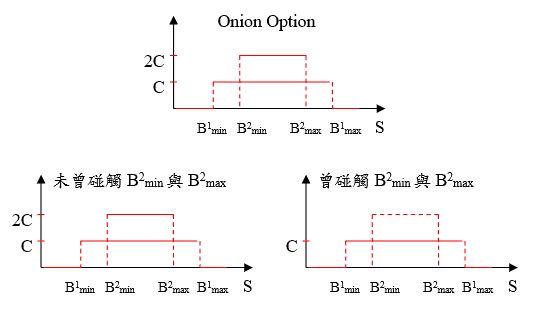
洋蔥選擇權形態上與結婚蛋糕 (Wedding Cake) 相仿,然而 Wedding Cake 只需要在到期日時股價停留在 B2min 與 B2max 之間即可拿到 2C 報酬,不論選擇權存續期間股價是否曾碰觸過其他障礙價位。而洋蔥選擇權則是當選擇權存續期間內,若未曾穿越 B2min 與 B2max 等價位,則到期可獲得 2C 報酬,若曾經碰觸過 B2min 與 B2max 等任一價位、且未曾碰觸過 B1min 與 B1max 等價位,即便到期日股價維持在 B2min 與 B2max 間,投資人依然只能獲得 C 報酬。在碰觸過障礙價位後即被一層層剝去報酬機會,因此被稱為洋蔥選擇權。此商品可拆解為買入兩個 Double-No-Touch Digitals:
Onion Option = DNTD(B1min, B1max) + DNTD(B2min, B2max)
結語
國際金融市場的成長速度日新月異,事實上,能夠使用融合法組裝的商品多不勝舉,讀者在運用這種方式創造新商品的同時,應把目標著重在「零成本」的商品架構上。藉由上述的介紹,即便發展中的發行商尚未具備「從無中生有」的創新商品能力,藉著對各式各樣商品、選擇權的廣泛了解,依然有機會能夠依靠「創意」、「想像力」,從中設計、組裝出各類型嶄新商品,進而增進其國際競爭力。
延伸閱讀 – 「Python – 繪製選擇權的收益曲線 (Payoff Diagram)」。
Reference
- Ebenfeld, S., Mayr, M. R., Topper, J., An Analysis of Onion Options and Double-no-Touch Digitals, Wilmott magazine, September 2002.
- Reiner, E., Rubinstein, M., Unscrambling the Binary Code. Risk, 4, October 1991.
- Wystup, U., FX Options and Structured Products. John Wiley & Sons, Ltd. 2006.

